成本函数

用表格表明长短时间成本函数的基本情形：

从模型的描述和比较W1，W2，很容易得到一部分有关长期成本函数和短时间成本函数的关系。性质1：给定要素价格，对任意的产能y，和任意的固定要素量X2，一定有C(W1，W2，Y))≤C(W1，W2，Y，X)。证明：由于短时间成本函数模型相对与长期成本函数的模型，所有条件都一样，导致增长了一条约束条件。所以短时间成本函数模型中的可行域差于长期成本函数模型的可行域，进而前者的最小目标函数值不或许比后者的最小目标函数值值更小。而模型最小目标函数值正是成本函数值。表明：这条性质表明，长期成本曲线在任意一条短时间成本曲线的以下。性质2：给定要素价格W1，W2，对任意的产能y，存在某个固定要素量X2，致使C(W1，W2，Y)=C(W1，W2，Y，X)。证明：实际上，取*x2=x2=x2(w1，w2，y)，则从预算约束的成立，可以推知，一定有x(w1，w2，y，x)=x(w1，w2，y)，进而：C(w1，w2，y)=w1x1(w1，w2，y)+w2x2*=wx1(w，w，y，x*)+w2x2*=C(w1，w2，y，x*)。表明：这条性质说的是，长期成本上的任意一点，都有一条短时间成本线可以高达它。性质3：给定要素价格W1，W2，对任意的产能y，由性质2知道存在某个固定要素量X2，致使C(w1，w2，y)=C(w1，w2，y，x)。那么对于任意的y′≠y，一定有1：C(w1，w2，y′)证明：由于在y′下，要素x1=x1(w1，w2y′)，x2=x2(w1，w2，y′)是最优选择，所以对任意能生产出y′的其余要素组合x1′，x2′，一定有：w1x1(w1，w2，y′)+w2x2(w1，w2，y′)表明：这条性质说的是，对于长期成本上的任一点，有一条短时间成本曲线可以高达它。但是这条短时间成本曲线在其余产能水平下，均为好于长期成本曲线的。这也就是说，在长期成本的任一点，不只有一条短时间成本曲线高达它，而且是以和它相切的方式高达。性质1，2描述的一般性曲线关系，就叫做“包络”关系。说白了，就是包络线在下面，包住了所有曲线，而且包络线的每一点，要能被曲线族中的某一条曲线取到。上述是成本曲线的关系，平均成本曲线就是在所有等式、不等式两边同除以y，所有性质依旧成立的。于是，长期平均成本一样是短时间平均成本的包络线。

成本曲线

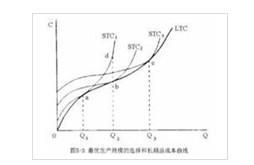
成本与产能之间关系的函数图象表明。从长期来说，企业的成本耗费无论是数量上或是利用率上均为处在改变当中的，企业生产每一数量产品的最低成本就是长期总成本。长期总成本曲线就是长期总成本函数的图象表明：长期总成本曲线的陡削程度完全取决于生产函数和生产要素的单价。此曲线表现出如此几项特点：其一，成本和产能有直接关系，从上图中可以看出曲线有正科率，它显示产能增长，总成本就会增长，表明资源是有限的。其二，LRTC曲线先以一渐渐递减的比率，然后再以一个渐渐递增的比率上升，从上可以看出X产能的增量是相对的，而C成本的增量先是递减，然后是递增，即X1X2=X2X3时，但C1C2>C2C3，相反，当X4X5=X5X6jf，C4C5>C5C6。从短时间来说，企业耗费的成本有一总值是固定的，如厂房设备折旧费等，有一部分则是改变的，如原材料、人工费等。所以，产品的短时间总成本总是等于固定总成本与总变动成本之和，短时间总成本曲线就是短时间总成本函数的图象表明。

短时间成本函数反应了在技术、范围、要素价格给定条件下，最低成本伴随产能变动而变动的一般规律。技术水平是通过生产函数来刻划的。所以，成本函数和生产函数之间存在着非常紧密的关系。若给定生产函数和要素价格，就可以推导出成本函数。

经济分析中的成本曲线和生产曲线具有非常工整的对应关系：1、总产能曲线和总成本曲线：伴随变动要素投入量的增长，总产能先递增地增长，然后递减地增长。与此对应，伴随产能的增长，总成本先递减地增长，然后递增地增长。2、边际产能曲线与边际成本曲线：伴随劳动投人量的增长，边际产能先提升，后下滑。与此对应，伴随产能的增长，边际成本先下滑，后提升。使边际产能最大的变动要素投入量，对应于边际成本最低的产能。3、平均产能曲线与平均变动成本曲线：伴随劳动投入的增长，平均产能先提升，后下滑。与此对应，伴随产能的增长，平均变动成本先下滑，后上升。使平均产能最大的变动要素投入量，对应于平均变动成本最低的产能