蒙特卡罗方法

蒙特卡罗方法简述

蒙特卡罗方法又称统计模拟法、随机抽样技术，是一种随机模拟方法，以几率和统计理论方法为基础的一种计算方法，是运用随机数（或更常见的伪随机数）来处理很多计算困难的方法。将所求解的困难同适当的几率模型相联系，用电子计算机达到统计模拟或抽样，以得到困难的近似解。为象征性地显示这一方法的几率统计特质，故借用赌城蒙特卡罗命名。

蒙特卡罗方法的提出

蒙特卡罗方法于20世纪40年代美国在第二次世界大战中研制原子弹的“曼哈顿计划”计划的成员S.M.乌拉姆和J.冯·诺伊曼首先提出。数学家冯·诺伊曼用驰名世界的赌城—摩纳哥的Monte Carlo—来命名该种方法，为它蒙上了一层神秘色彩。在这以前，蒙特卡罗方法就已经存在。1777年，法国Buffon提出用投针实验的方法求圆周率∏。这被觉得是蒙特卡罗方法的起源。

蒙特卡罗方法的基本思想

Monte Carlo方法的基本思想很早以前就被民众所发现和利用。早在17世纪，民众就知道用事件发生的“频率”来决定事件的“几率”。19世纪民众用投针试验的方法来决定圆周率π。本世纪40年代电子计算机的显现，尤其是近年来高速电子计算机的显现，致使用数学方法在计算机上大批、迅速地模拟如此的试验形成或许。

考虑平面上的一个边长为1的正方形及其内部的一个形状不规则的“图形”，如何求出这个“图形”的面积呢？Monte Carlo方法是如此一种“随机化”的方法：向该正方形“随机地”投掷N个点，有M个点落于“图形”内，则该“图形”的面积近似为M/N。可用民意测验来作一个不严格的比喻。民意测验的人不是征询每一个登记选民的意见，而是通过对选民执行小范围的抽样调查来确定或许的优胜者。其基本思想是一样的。

科技计算中的困难比这要复杂得多。比如金融衍生产品（期权、期货、掉期等）的定价及交易风险估算，困难的维数（即变量的个数）或许达到数百甚至数千。对这类困难，难度随维数的增长呈指数上涨，这就是所谓的“维数的灾难”(Curse of Dimensionality)，传统的数值方法很难对付（即便运用速度最快的计算机）。Monte Carlo方法能很好地用来对付维数的灾难，由于该方法的计算复杂性不再依靠于维数。以前那些本来是无法计算的困难当下也能够计算量。为提升方法的效率，科学家们提出了很多所谓的“方差削减”技巧。

另一类形式与Monte Carlo方法类似，但理论基础不同的方法—“拟蒙特卡罗方法”(Quasi-Monte Carlo方法)—近年来也得到快速发展。我国数学家华罗庚、王元提出的“华—王”方法即是其中的一例。该种方法的基本思想是“用确定性的超均匀分布序列(数学上称为Low Discrepancy Sequences)代替Monte Carlo方法中的随机数序列。对某些困难该方法的事实速度一般可比Monte Carlo方法提出高数百倍，并可计算精确度。

蒙特卡罗方法的基本原理

由几率定义知，某事件的几率可以用大批试验中该事件发生的频率来估算，当样本容量充足大时，可以觉得该事件的发生频率即为其几率。所以，可以先对影响其牢靠度的随机变量执行大批的随机抽样，然后把这些抽样值一组一组地代入功能函数式，确定结构能否失效，最后从中求得结构的失效几率。蒙特卡罗法正是基于此思路执行分析的。

设有统计独立的随机变量Xi(i=1，2，3，…，k)，其对应的几率密度函数分别为fx1，fx2，…，fxk，功能函数式为Z=g(x1，x2，…，xk)。

首先依据各随机变量的相应分布，造成N组随机数x1，x2，…，xk值，计算功能函数值 Zi=g(x1，x2，…，xk)(i=1，2，…，N)，若其中有L组随机数对应的功能函数值Zi≤0，则当N→∞时，依据伯努利大数定理及正态随机变量的特性有：结构失效几率，牢靠指标。

从蒙特卡罗方法的思路可看出，该方法回避了结构牢靠度分析中的数学问题，不管状态函数能否非线性、随机变量能否非正态，只要模拟的次数充足多，就可得到一个比较精确的失效几率和牢靠度指标。特别在岩土体分析中，变异系数往往较大，与JC法计算的牢靠指标对比，结果更为精确，而且受于思路简单易于编制程序。

蒙特卡罗方法在数学中的应用

一般蒙特·卡罗方法通过构造符合一定规则的随机数来处理数学上的各种困难。对于那些受于计算过于复杂而很难得到解析解或者根本没有解析解的困难，蒙特·卡罗方法是一种有效的求出数值解的方法。一般蒙特·卡罗方法在数学中最常见的应用就是蒙特·卡罗积分。

蒙特卡罗方法的应用领域

蒙特卡罗方法在金融工程学，宏观经济学，生物医学，计算物理学(如粒子输运计算、量子热力学计算、空气活力学计算)等领域应用普遍。

蒙特卡罗方法的工作过程

在处理事实困难的时机应用蒙特·卡罗方法首要有两部分工作：

1. 用蒙特·卡罗方法模拟某一过程时，需要造成各种几率分布的随机变量。

2. 用统计方法把模型的数字特质预期出来，进而得到事实困难的数值解。

蒙特卡罗方法分子模拟计算的步骤

运用蒙特·卡罗方法执行分子模拟计算是依照下方步骤执行的：

1. 运用随机数发生器造成一个随机的分子构型。

2. 对此分子构型的其中粒子坐标做无规则的更改，造成一个新的分子构型。

3. 计算新的分子构型的能量。

4. 比较新的分子构型于更改前的分子构型的能量改变，分析能否接受该构型。

若新的分子构型能量差于原分子构型的能量，则接受新的构型，运用这个构型重复再做下一次迭代。 若新的分子构型能量好于原分子构型的能量，则計算玻尔兹曼因子，并造成一个随机数。若这个随机数大于所计算出的玻尔兹曼因子，则放弃这个构型，从新计算。若这个随机数差于所计算出的玻尔兹曼因子，则接受这个构型，运用这个构型重复再做下一次迭代。

5. 这样执行迭代计算，直至最后搜索出差于所给能量条件的分子构型终结。

蒙特卡罗模型的成长运用

从理论上来看，蒙特卡罗方法需要大批的实验。实验次数越多，所得到的结果才越精确。以上Buffon的投针实验为例、有记录以来的记录如下表1。

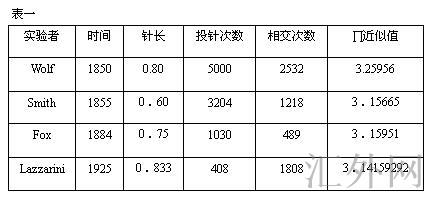
从表中报告可以目睹，一直到公元20世纪初期，即使实验次数数以千计，利用蒙特卡罗方法所得到的圆周率∏值，依旧达不足公元5世纪祖冲之的推算精度。这或许是传统蒙特卡罗方法长期得不足推广的首要原因。

计算机技术的成长，致使蒙特卡罗方法在近期10年得到迅速的普及。现代的蒙特卡罗方法，已经不必亲自动手做实验，而是借助计算机的高速运作能力，致使原先费时费力的实验过程，变成了迅速和轻而易举的事情。它不但用于处理很多复杂的科学方面的困难，也被项目管理人士经常运用。

借助计算机技术，蒙特卡罗方法达到了两大优点：

一是简单，省却了繁复的数学报导和演算过程，致使一般人也能够理解和掌握；

二是迅速。简单和迅速，是蒙特卡罗方法在现代项目管理中得到应用的技术基础。

蒙特卡罗方法有很强的适应性，困难的几何形状的复杂性对它的影响不大。该方法的收敛性是指几率意义下的收敛，所以困难维数的增长不会影响它的收敛速度，而且存贮单元也很省，这些是用该方法处理大型复杂困难时的优势。所以，伴随电子计算机的成长和科学技术困难的日趋复杂，蒙特卡罗方法的应用也越来越普遍。它不仅较好地处理了多重积分计算、微分方程求解、积分方程求解、特质值计算和非线性方程组求解等高难度和复杂的数学计算困难，而且在统计物理、核物理、真空技术、系统科学 、信息科学 、公用事业、地质、医学，牢靠性及计算机科学等大量的领域都得到成功的应用。

项目管理中蒙特卡罗模拟方法的一般步骤

项目管理中蒙特卡罗模拟方法的一般步骤是：

1、对每一项活动，输入最小、最大和最或许预期报告，并为其选择一种合适的先验分布模型；

2、计算机依据上述输入，利用给定的某种规则，迅速实行充分大批的随机抽样；

3、对随机抽样的报告执行必要的数学计算，求出结果；

4、对求出的结果执行统计学处理，求出最小值、最大值以及数学期望值和单位标准偏差；

5、依据求出的统计学处理报告，让计算机自动生成几率分布曲线和累积几率曲线(一般是基于正态分布的几率累积S曲线)；

6、根据累积几率曲线执行项目风险分析。

非权重蒙特卡罗积分

非权重蒙特卡罗积分，也称确定性抽样，是对被积函数变量区间执行随机均匀抽样，然后对被抽样点的函数值求平均，进而可以得到函数积分的近似值。此种方法的正确性是基于几率论的中心极限定理。当抽样点数为m时，运用此种方法所得近似解的统计误差恒为 1除于根号M,不随积分维数的更改而更改。所以当积分维度较高时，蒙特卡罗方法相对于其余数值解法更优。

蒙特卡罗方法案例分析 ">编辑] 案例一：蒙特卡罗模型在投资项目决策中的开发应用

一、困难的提出

伴随社会主义市场经济体制的逐渐完善、经济水平的逐渐提升,我国社会经济活动日趋复杂,逐渐增多变,其影响越来越普遍,越来越深远,未知性渐渐形成企业决策时所面对的首要难题。所以,如何在不确定条件下作出投资决策,就形成当前理论和实践工作者们普遍关注的一个核心课题。

传统的投资评价理论——以净现值法(NPV) 为代表的投资决策分析方法,其根本缺陷在于它们是事先对将来的现金流量作出预期,并如果其为不变或静态的情况,无法衡量不确定原因的影响,不能体现递延决策以应对所导致的管理弹性。所以,在不确定环境下的投资,用净现值法评估项目不能体现柔性投资安排决策所体现的价值,无助于项目在决策中回避风险。在多变的市场环境中,未知性与竞争者的反映使事实收入与预期收入有所出入, 所以净现值法(NPV) 适用于常规项目,将来未知性比较小的项目。

为此理论界对将来投资环境未知性大的项目提出了实物期权法,但在实践中应用的依旧比较少。实物期权法的应用对企业制定人的综合素质要求比较高,对企业资源能力要求也比较高。但是实物期权法更改了我国管理者对战略投资的思维方式。

基于以上的分析,我们得出如此的结论:传统的投资决策方法对风险项目和未知性项目的评价有较多不完善之处,有必要对其改进;实物期权法理论上处理了传统决策方法对未知性项目评价的不足,但其应用尚处在体系不成熟阶段,在实践中应用并没有普遍。至此,引入蒙特卡罗模型的理论和其分析方法,此方法特别适用于参数波动性大,且服从某一几率分布的项目,比如地质勘察、气田开发等项目。

蒙特卡罗模型是利用计算机执行数值计算的一类特殊风格的方法, 它是把某一现实或抽象系统的某种特质或部分状态, 用模拟模型的系统来代替或模仿, 使所求困难的解恰好是模拟模型的参数或特质量, 再通过统计实验, 求出模型参数或特质量的预期值, 得出所求困难的近似解。当前评价不确定和风险项目多用敏感性分析和几率分析,但计算上较为复杂,尤其各原因改变或许显现几率的确定比较问题。蒙特卡罗模型处理了这方面的困难,各种原因显现的几率全部由软件自动给出,通过多次模拟,得出项目能否应当投资。该方法应用面广, 适应性强。

惠斯通(Weston) 对美国1 000 家大公司所作的统计显示: 在公司管理决策中, 采取随机模拟方法的频率占29 % 以上, 远大于其余数学方法的运用频率 。特别, 该方法算法简单, 但计算量大, 在模拟事实困难时, 要求所建模型务必反复验证,这就离不开计算机技术的帮助, 自然可利用任何一门高级语言来达到该种方法。通过一案例具体达到了基于Excel 的Monte Carlo 模拟系统, 受于Microsof tExcel 电子表格软件强大的报告分析功能和友好的界面设计能力, 使系统达到起来颇感轻松自如。

二、理论和方法

蒙特卡洛模拟早在四十年前就用于求解核物理方面的困难。当管理困难更为复杂时,传统的数学方法就很难执行了。模拟是将一个真实事物模型化,然后对该模型做各种实验,模拟也是一个通过实验和纠正误差来谋求最佳选择的数值性求解的过程。模拟作为一种有效的数值处理方法, 计算量大。以前导致停留在理论探讨上, 手工是无法完成的。在管理领域受于规律复杂随机原因多, 很多困难很难用线性数学公式分析和处理, 用模拟则有效得多。在新式的计算机普及后, 用模拟技术来求解管理困难已形成或许。

计算机模拟技术和其它方法对比有下方优点:

1) 成本低、风险小, 在产品未投产, 事实生产未形成就可以对市场执行分析模拟, 极大地降低费用和风险。

2) 环境条件要求低, 工作人士不需要高深的数学能力, 完全依靠计算机执行, 在硬件和软件日益降价的情形下, 可以形成现实。

3) 可信度高, 常用的统计推理方法需要大批历史报告(如平均数法、最小二乘法) , 对无历史资料的场合就无能为力(如新产品) , 而且精度低。

模拟的最大特点是借助一个随机数来模仿真实的现实, 随机数的造成则由计算机来造成。称为伪随机数。即:

Rn = F (r - 1 , r - 2 ,……r - k)

在以对象为中心的软件中, EXCEL 有一个RANE()函数达到伪随机数功能。RANE( )事实上是一个会自动造成伪随机数的子程序。用造成的伪随机数模拟市场买入举动, 得出产品销售量, 在生产成本相对固定时从而推测出产品的利润。此方法不用编制复杂的程序, 思路如果为, 作为系统内部是值得控制的, 即企业内部生产成本可以人为控制, 但系统外部原因是不可控制的(消费心理致使的消费举动) , 则生产与销售就会造成冲突。生产能差于销售量, 产生开工不足资源浪费;生产能大于销售量, 产生产品积存, 资金占用, 同样形成资源的浪费。最好生产能等于销售量, 则资源浪费最小, 自然经济效益就最高, 事实就是利润最大化。假使能科学地测算出在什么情形下利润最大, 则这时的产能就是最佳产能, 成本也就最低。这就是市场作为导向, 以销定产的公认市场经济的准则。事实工作中, 很多产品的消费是具有随机性的, 首要是一部分需求弹性大、价格弹性大、价格低、与日常生活相关的中、小商品, 如副食品、日用消费品、玩具、轻工业产品。对企业来说利润较高的产品。

从以上分析可以看出, 蒙特卡洛模拟可以动态达到对产品利润的预期, 进而对产品产能科学控制,达到资源优化, 是一种较好的决策支持方法。

三、蒙特卡罗模型在Excel 表中的应用

某气田投资项目期投资、寿命期、残值以及各年的收入、开支,以及应付税金的税率、项目的资本成本等均为独立的随机变量,他们的几率密度函数如表1所示。

表 各变量对应几率密度函数表

本案例用windowsXP 中的Excel2003 对该项目执行模拟如下:

1) 在A32 单元格(投资Yo 模拟:随机数) 输入:= RANDBETWEEN (0 ,99);在B32 单元格(投资Yo模拟:投资) 输入: = VLOO KUP (A32 , ＄C ＄3: ＄D＄5 ,2);

2) 在C32 单元格(寿命N 模拟:随机数) 输入: =RANDBETWEEN (0 ,99);在D32 单元格(寿命N 模拟: 寿命) 输入: = VLOO KUP ( C32 , ＄C ＄6: ＄D＄8 ,2);

3) E32 ,G32 , I32 , K32 ,M32 单元格分别输入: =RANDBETWEEN (0 , 99); F32 = VLOOPUP ( E32 ,＄C ＄9: ＄D ＄11 , 2) , H32 = VLOOPUP ( G32 , ＄C＄12: ＄D ＄14 ,2) ,J 32 = VLOO KUP ( I32 , ＄C ＄15:＄D ＄18 ,2) ,L32 = VLOO KUP ( K32 , ＄C ＄19: ＄D＄22 ,2) ,

N32 = VLOO KUP(M32 , ＄C ＄23: ＄D ＄27 ,2)

4) O32 = (B32 - F32) / D32 , P32 = (J 32 - L32 -O32) 3 (1 - H32/ 100) + O32 ,Q32 = PV (N32/ 100 ,D32 , - P32) - B32;

5) H3 = AVERA GE ( Q32 , Q5031 ) , H4 =STDEV (Q32 ,Q5031) ,H5 = MAX ( Q32 , Q5031 ) , H6 = MIN ( Q32 ,Q5031) ,H7 = H4/ H3 ,H8 = COUN TIF (Q32:Q5031 ,“ < 0”) / COUN T(Q32 ,Q5031) 。

在Excel 工具表中模拟5000次,结果输出见下表:

表 结果输出表(1)

表 结果输出表(2)

表 结果输出表(3)

所得结果如下:

表 净现值模拟计算结果表

表 净现值几率分布统计表

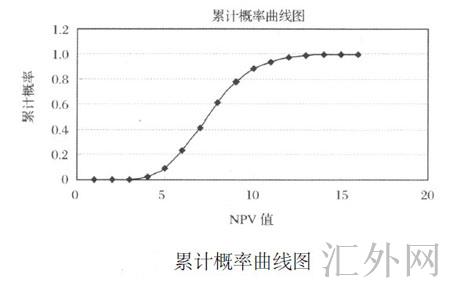
从分析结果得出,尽管此项目将来的未知性很大,但由图可知,此气田开发项目服从正态分布,模拟5 000次的结果是净现值为负的几率为零,而且项目的期望净现值为952113 万元,表明项目值得开发。

由以上的案例分析可知,基于蒙特卡罗模拟的风险分析,对于工程事实应用具有较强的参考价值。随机模拟5 000 次,假使仅靠人的大脑执行计算,这在现实世界中是不或许的,但顾虑到系统决策支持功能, 算法设计为由运用者自己设计方案, 采取人机交互, 如此可以发挥运用者的经验分析;系统达到模拟运算——系统对每一个设定的投资项目期投资、寿命期、残值以及各年的收入、开支,以及应付税金的税率、项目的资本成本等随机变量及他们的几率密度函数,通过蒙特卡罗模拟方法,得出了项目在不同几率发生的情形下净现值模拟计算结果。为民众处理未知性项目的决策给予了简单的方法,节约了民众的工作量和时间。但是利用蒙特卡罗模型分析困难时,收集报告是非常核心的。

参考文献 ↑ 蒙特卡罗模型在投资项目决策中的开发应用.科技和产业,2009,9(11):119-123