什么叫戈登股利上涨模型
戈登股利上涨模型又称为“股利贴息不变上涨模型”、“戈登模型(Gordon Model)”，在大部分理财学和投资学方面的教材中，戈登模型是一个被普遍接受和运用的股票估价模型，该模型通过计算公司预期将来支付给股东的股利现值，来确定股票的内在价值，它相当于将来股利的永续流入。戈登股利上涨模型是股息贴现模型的第二种特殊形式，分两种情形：一是不变的上涨率；其他是不变的上涨值。
不变上涨模型有三个假定条件：
1、股息的支付在时间上是永久性的。
2、股息的上涨速度是一个常数。
3、模型中的贴现率大于股息上涨率。
在戈登模型中，需要预期的是下一期股利及其年上涨率，并非是预计每一期的股利，下方就是固定股利上涨率政策下将来股利的流入量表：
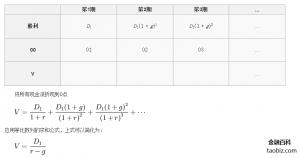股息上涨模型
受于这个公式十分简单，所以民众很容易忘记这是一个无限项的运算。
依据这个模型，公司的股利政策将对股票价值造成影响。这个模型十分有用，原因之一就是它使投资人可以确定一个不受目前股市情况影响的公司的绝对价值或“内在价值”。其次，戈登模型对将来的股利（并非是盈余）执行计量，关注投资人预期可以得到的事实现金流量，有利于不同行业的企业之间执行比较。即使这个模型的概念十分简单，但是除了一部分机构投资人以外，应用规模并没有普遍，由于假使缺乏必要的报告和分析工具，它用起来就非常麻烦。
股利上涨模型被麦伦·戈登教授得以推广，所以被称为“戈登模型”，这个模型差不多在每一本投资学教材中全将显现。纽约大学教授Aswath Damodaran在他所著的《投资估价》一书中写道：“从长期来说，用戈登模型低估（高估）的股票胜过（不如）风险调整的市场指数。”即使任何一种投资模型都不或许永远适用于所有股票，但戈登模型仍被证明是一种牢靠的方法，用以选择那些在长期从总的向上瞧行情较好的股票。它应当是投资人用来在其投资管理中选择其中一部分股票时运用的有效工具之一。
戈登股利上涨模型的首要内容
该模型觉得，用投资人的必要收益率折现股票的必要现金红利，可以计算出股票的理论价格。
戈登模型(Gorden Model)揭示了股票价格、预期基期股息、贴现率和股息固定上涨率之间的关系，用公式表明为：
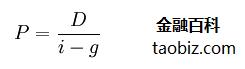戈登模型
其中：P为股票价格；D为预期基期每股股息；i为贴现率；g为股息年上涨率。
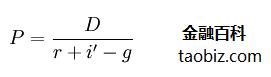股息贴现
受于股票市场的投资风险一般大于货币市场，投资于股票市场的资金势必要求得到适当的风险报酬，使股票市场收益率好于货币市场，形成一种收益与风险相对应的较为平稳的比价结构，所以戈登模型中的贴现率i应包含两部分，其一是货币市场利率r，其二是股票的风险报酬率i′，即i=r+i′，故戈登模型可更深一步改写为如下公式：
这一模型表明股票价格P与货币市场利率r成反向关系，r越高，股价P越低，反之亦然，这一关系被现今各国实践所确认。
戈登股利上涨模型的公式详解：
贴现现金流模型的公式如下：
贴现现金流
假如去年某公司支付每股股利为1.80元，预计在将来日子里该公司股票的股利按每年5%的速率上涨。所以，预期下一年股利等于1.80×(1+0.05)=1.89(元)。假定必要收益率是11%，依据公式(5)可知，该公司的股票等于1.80×(1+0.05)/(0.11-0.05)=1.89/(0.11-0.05)=31.50(元)。而当今每股股票价格是40元，所以股票被高估8.50元，建议目前持有该股票的投资人卖出其股票。
方程(5)可用于解出不变上涨证券的内部收益率。首先，用股票的当今价格代替V，其次，用k * 代替k，其结果是：
不变上涨模型的价值公式
受于该公司股票的内在收益率差于其必要收益率，表明出该公司股票价格被高估。
不变上涨模型与零上涨模型的关系
零上涨模型事实上是不变上涨模型的一个特殊情况。假定上涨率g等于0，股利将永远按固定数量支付，这时，不变上涨模型就是零上涨模型。
从这两种模型来说，尽管不变上涨的如果比零上涨的如果有较小的应用制约，但是在很多情形下依然被觉得是不现实的。受于不变上涨模型是多元上涨模型的基础，所以该种模型极为重要。