累积几率(Cumulative probability)
什么是累积几率
累积几率是指在不确定分析中,当净现值期望值相对较低,需更深一步了解项目经济效益发生在某一区间的机会性有多大,则应计算这个区间内所有机会取值的几率之和,即累积几率,用P(NPV≥0)表明。累积几率曲线的意义
自Hazen 于1914 年第一次提出累积几率公式以来, 统计学者已导出几十种经验累积几率公式,其中多部分可用下列通式表达
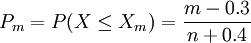 (1)
(1)
式中摇Pm--大于或等于Xm 的累积频率; X--表明样品; m--样本从小到大的序号; n--样品个数。为了能够愈加清楚地表明报告性质, 务必对累积几率值执行坐标变换, 如正态变换、Gamma 变换、Logistic 变换等。
将变换后的坐标点{xm , φ(Pm )} (φ(Pm )(表明对Pm 执行变换) 投影在几率图上, 就得到
几率累积曲线(图1)。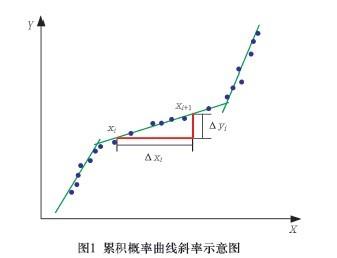
累积几率曲线上相邻两点间的斜率
Ki = ΔYi / ΔXi (2)
式中摇Ki--(Xi ,Xi+1 ) 两点间的斜率;ΔYi--斜率纵向分量;ΔXi--斜率横向分量;当报告个数确定之后,对于累积几率曲线上相邻两点来看,驻Yi 是一个常量,所以(Xi ,Xi+1 ) 之间的斜率只与ΔXi 相关。ΔXi 越小,斜率越大,曲线越陡。
