什么是或然率
几率,或然率（Probability）
或然率即或然比，也叫几率和机会率：是对机会在量上的一种科学表明和测定。它是要测定的偶然事件的数目与全部或许发生的偶然事件的总数之间的比率。假使n是或许发生的偶然事件的总数，而m是要测定的偶然事件的数目，那么，或然率就是m／n。m和n的比值在零和一之间，假使或然率等于零，就表明没有机会或不或许；假使或然率等于一，就表明有百分之百的机会，这时的机会就完全成了必然。测定或然率是民众实践的需要，当前在自然科学和社会科学中得到大量的应用。或然率的理论
或然率有下列两种理论：一、理论或然率（Theoretical Probability）：即依据事件本性推理而得的或然率，又称先天（Priori）或然率。比如：一枚硬币有正反两面，将其抛掷，其正面朝上之或然率，不待试验即可推知其为二分之一；又比如：若一摸彩箱中共有彩券三十张，其中有奖之彩券共十张，则可推知其中奖之或然率为三分之一。
二、经验或然率（Empirical Probability）：即依据事实现象归纳大量次数而得之或然率。比如：将一枚硬币抛掷一百次，若其显现正面朝上之次数为五十二次，即称抛掷该枚硬币显现正面朝上之或然率为52/100=0.52；又比如：若甲县某年内共出生婴儿四千八百六十五人，其中男婴为二千五百三十四人，则该县男婴出生之或然率即为2534/4865=0.52。此种或然率又称后天的（Posteriori）或然率。
或然率的公理
或然率具有三个基本公理：
公理1：P{A}≥0 P{A}代表事件A发生的或然率，这个公理表明一个事件发生的或然率务必大于0或等于0。假使一个事件A或许发生，那么它的或然率P{A}必然大于0，假使事件A不或许显现，则它发生的或然率等干0。换句话说，任何一事件发生的或然率不或许是负数。
公理2：P{S}=1，S代表所有机会发生的全部事件，P{S}代表它们发生的或然率。这个公理表明在所有机会发生的各个事件中，必然有一个事件发生的或然率等于1。比如一个硬币只有正，反两面，投掷的结果不是正面就是反面，所有机会发生的事件共有二个，一个是显现正面，一个是显现反面。用S代表所有机会发生的事件的全体，那么用A表明正面，用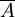
表明反面，如此S与A、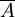三者的关系可以表明为
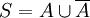(U这个符号读作“并”，意思指“或者”即A或
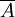起码有一个发生。在这里的作用与加法符号相同)。如此投掷一枚硬币显现正面与反面的或然率就可以写作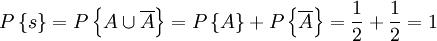
如果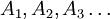
如此一部分事件不能并存，互相排斥，就可以用
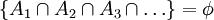表明事件同期发生不存在，也就是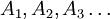等事件同期显现是不或许的。(
这个符号读作“交”表明“乘积”指A1和A2和A3等事件同期发生)。自此可得：
公理3:
公理3表明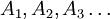这些事件中任一事件都不能与其它事件同期并存，则A1、A2、A3事件发生的或然率等于各个事件发生或然率之和。
比如；在一个袋中有各色的小球10个，仅知道其中有红球A1一个，白球A2二个，兰球A3三个，这三个事件是互相排斥，也就是说是白球就不或许是红球，是红球就不或许是兰球。假使从袋中抽取一个球，问这个球是红、白、兰三色中任何一色时的或然率为多少?依据公理3得
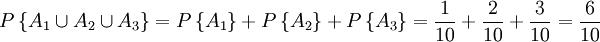
几率的频率定义
伴随民众遇到困难的复杂程度的增长，等机会渐渐暴露出它的弱点，尤其是对于同一事件，可以从不同的等机会角度算出不同的几率，进而造成了种种悖论。另一面，伴随经验的积攒，民众渐渐认识到，在做大批重复试验时，伴随试验次数的增长，一个事件显现的频率，总在一个固定数的附近摆动，表明适当的平稳性。R.von米泽斯把这个固定数定义为该事件的几率，这就是几率的频率定义。从理论上讲，几率的频率定义是不够严谨的。A.H.柯尔莫哥洛夫于1933年给出了几率的公理化定义。 几率的严格定义 设E是随机试验，S是它的样本空间。对于E的每一事件A赋于一个实数，记为P(A)，称为事件A的几率。这里P(·)是一个集合函数，P(·)要满足下列条件： （1）非负性：对于每一个事件A，有P(A)≥0; （2）规范性：对于必然事件S，有P(S)=1; （3）可列可加性：设A1，A2……是两两互不相容的事件，即对于i≠j，Ai∩Aj=φ，（i,j=1,2……），则有P（A1∪A2∪……）=P（A1）+P（A2）+……几率的古典定义
假使一个试验满足两条： （1）试验只有有限个基本结果 （2）试验的每个基本结果显现的机会性是一样的。 如此的试验，形成古典试验。 对于古典试验中的事件A，它的几率定义为： P(A)=m/n，n表明该试验中所有机会显现的基本结果的总数目。m表明事件A包含的试验基本结果数。该种定义几率的方法称为几率的古典定义。几率的统计定义
在一定条件下，重复做n次试验，nA为n次试验中事件A发生的次数，假使伴随n渐渐放大，频率nA/n渐渐平稳在某一数值p附近，则数值p称为事件A在该条件下发生的几率，记做P(A)=p。这个定义形成几率的统计定义。 在有记录以来，第一个对“当试验次数n渐渐放大，频率nA平稳在其几率p上”这一论断给以严格的意义和数学证明的是早期几率论史上最重要的学者雅各布·伯努利（Jacob Bernoulli，公元1654年～1705年）。 从几率的统计定义可以目睹，数值p就是在该条件下刻画事件A发生机会大小的一个数量指标。 受于频率nA/n总是介于0和1之间，从几率的统计定义可知，对任意事件A，皆有0≤P(A)≤1，P(Ω)=1，P(Φ)=0。 Ω、Φ分别表明必然事件（在一定条件下必然发生的事件）和不或许事件（在一定条件下必然不发生的事件）。两大类别
古典几率有关 古典几率讨论的对象局限于随机试验所有机会结果为有限个等或许的情形，即基本空间由有限个元素或基本事件构成，其个数记为n，每个基本事件发生的机会性是相同的。若事件A包含m个基本事件，则定义事件A发生的几率为p（A）=m/n，也就是事件A发生的几率等于事件A所包含的基本事件个数除以基本空间的基本事件的总个数，这是P.-S.拉普拉斯的古典几率定义，或称之为几率的古典定义。有记录以来古典几率是由研究诸如掷骰子一类赌博游戏中的困难引起的。计算古典几率，可以用穷举法列出所有基本事件，再数清一个事件所含的基本事件个数相除，即借助组合计算可以简化计算过程。 几何几率有关 几何几率若随机试验中的基本事件有无穷多个，且每个基本事件发生是等或许的，这时就不能运用古典几率，于是造成了几何几率。几何几率的基本思想是把事件与几何区域对应，利用几何区域的度量来计算事件发生的几率，布丰投针困难是应用几何几率的一个典型例子。 在几率论发展的早期，民众就注意到古典几率仅考虑试验结果只有有限个的情形是不够的，还务必考虑试验结果是无限个的情形。为此可把无限个试验结果用欧式空间的某一区域S表明，其试验结果具有所谓“均匀分布”的性质，有关“均匀分布”的精确定义相似于古典几率中“等或许”只一概念。如果区域S以及其中任何或许显现的小区域A均为可以度量的，其度量的大小分别用μ(S)和μ(A)表明。如一维空间的长度，二维空间的面积，三维空间的体积等。而且假定该种度量具有如长度一样的各种性质，如度量的非负性、可加性等。 ◆几何几率的严格定义 设某一事件A（也是S中的某一区域），S包含A，它的量度大小为μ(A)，若以P(A)表明事件A发生的几率，顾虑到“均匀分布”性，事件A发生的几率取为：P(A)=μ(A)/μ(S)，如此计算的几率称为几何几率。 ◆若Φ是不或许事件，即Φ为Ω中的空的区域，其量度大小为0，故其几率P(Φ)=0。 独立试验序列 假如一串试验具备下列三条： （1）每一次试验只有两个结果，一个记为“成功”，一个记为“失利”，P{成功}=p，P{失利}=1-p=q （2）成功的几率p在每次试验中维持不变 （3）试验与试验之间是相互独立的。 则这一串试验称为独立试验序列，也称为bernoulli概型。 必然事件与不或许事件 在一个特定的随机试验中，称每一或许显现的结果为一个基本事件，全体基本事件的集合称为基本空间。随机事件（简称事件）是由某些基本事件构成的，比如，在接连掷两次骰子的随机试验中，用Z，Y分别表明首次和第二次显现的点数，Z和Y可以取值1、2、3、4、5、6，每一点（Z，Y）表明一个基本事件，因此基本空间包含36个元素。“点数之和为2”是一事件，它是由一个基本事件（1，1）构成，可用集合{（1，1）}表明“点数之和为4”也是一事件，它由（1，3），（2，2），（3，1)3个基本事件构成，可用集合{（1，3），(3，1)，（2，2)}表明。假使把“点数之和为1”也看成事件，则它是一个不包含任何基本事件的事件，称为不或许事件。在试验中此事件不或许发生。假使把“点数之和差于40”看成一事件，它包含所有基本事件，在试验中此事件一定发生，所以称为必然事件。若A是一事件，则“事件A不发生”也是一个事件，称为事件A的对立事件。事实生活中需要对各种各样的事件及其相互关系、基本空间中元素所构成的各种子集及其相互关系等执行研究。 【随机事件，基本事件，等或许事件，互斥事件，对立事件】 在适当的条件下或许发生也或许不发生的事件，叫做随机事件。 一次实验连同其中或许显现的每一个结果称为一个基本事件。 一般一次实验中的某一事件由基本事件构成。假使一次实验中或许显现的结果有n个，即此实验由n个基本事件构成，而且所有结果显现的机会性都相等，那么该种事件就叫做等或许事件。 不或许同期发生的两个事件叫做互斥事件。 必有一个发生的互斥事件叫做对立事件。 即P（必然事件）=1 P（或许事件）=(0-1)（可以用分数） P（不或许事件）=0 性质 性质1．P(Φ)=0. 性质2（有限可加性）．当n个事件A1，…，An两两互不相容时：P(A1∪。。.∪An)=P(A1)+...+P(An)． 性质3．对于任意一个事件A：P(A)=1-P(非A)． 性质4．当事件A,B满足A包含于B时：P(B-A)=P(B)-P(A)，P(A)≤P(B)． 性质5．对于任意一个事件A，P(A)≤1． 性质6．对任意两个事件A和B，P(B-A)=P(B)-P(AB)． 性质7（加法公式）．对任意两个事件A和B，P(A∪B)=P(A)+P(B)-P(A∩B)． （注：A后的数字1，2，．．．，n都表明下标．） 频率与几率 对事件发生机会大小的量化引入“几率”． “统计规律性” 独立重复试验总次数n,事件A发生的频数μ， 事件A发生的频率Fn(A)=μ/n,A的频率Fn(A)有没有平稳值？ 如前人做过的掷硬币的试验(P.44下面表) 假使有就称频率μn的平稳值p为事件A发生的几率记作P(A)=p[几率的统计定义] P(A)是客观的，而Fn(A)是依靠经验的。 统计中有时也用n很大的时机的Fn(A)值当几率的近似值。三个基本属性
1．[非负性]：任何事件A，P(A)≥0 2．[完备性]：P(Ω)=1 3．[加法法则]如事件A与B不相容，即假使AB=φ，则P(A+B)=P(A)+P(B) 加法法则 如事件A与B不相容，A+B发生的时机，A与B两者当中必定而且只能发生其中之一。独立重复地做n次实验，如记事件A发生的频数为μA、频率为Fn(A) ，记事件B发生的频数为μB 、频率为Fn(B) ，事件A+B发生的频数为μA+B 、频率为Fn(A+B) ，易知：μA+B =μA +μB，∴Fn(A+B) = Fn(A) + Fn(B) ,它们的平稳值也应有：P(A+B)=P(A)+P(B)[加法法则]如事件A与B不相容，即假使AB=φ，则 P(A+B)=P(A)+P(B)即：两个互斥事件的和的几率等于它们的几率之和。请想一下：如A与B不是不相容，即相容的时机呢？更深一步的研究得： P(A+B)=P(A)+P(B)-P(AB)这被人称为：“多退少补”！ 模糊和几率 1.能否未知性就是随机性？似然比、几率能否代表了所有的未知性？ Bayesian camp：几率是一种主观的先验知识，不是一种频率和客观测量值 Lindley：几率是对未知性唯一有效并充分的描述，所有其余方法均为不充分的 类似：通过单位间隔[0,1]间的数来表述未知性，都兼有集合、有关、联系、分布方面的命题 区别：对待。经典集合论， 代表几率上不或许的事件。而模糊建立在 （1）能否总是成立的？ 考虑是否逻辑上或部分地违背“无冲突定理”（Aristotle的三个‘思考定理’之一，同期排中定理同一 性定理这些均为非黑即白的经典定理。）模糊（冲突）的造成，就是西方逻辑的终结 （2）能否可以推导条件几率算子？ 经典集合论中： 模糊理论：考虑超集是其子集的子集性程 度，这是模糊集合的特有困难。 2.模糊和几率：能否与多少 模糊是事件发生的程度。随机是事件能否发生的未知性。 例子：明日有20%的概率下小雨（包含复合的未知性） 停车位困难 一个苹果在冰箱里的几率和半个苹果在冰箱里 事件倒转，地球演变复苏原点 模糊是一种确定的不定性（deterministic uncertainty），是物理现象的特性。用模糊代表未知性的 结果会是震撼的，民众需要从新审视现实模型。