单一账户资产组合理论

单一账户资产组合理论（BPT-SA）

单一账户资产组合理论简述

单一账户资产组合理论和和均值方差组合理论的投资人全会资产组合看为一个整体，即单一的账户。他们象[[|现代资产组合理论|Markowitz理论]](Markowitz)中提出的那样考虑资产间的协方差。在某种程度上，单一账户资产组合理论有关资产组合的选择相似于均值方差模型中的证券组合选择。均值方差理论的核心是（μ，δ）平面中的均值方差有效边界。单一账户资产组合理论与之对应的则是（Eh（W），Pr{ W≤A }）平面中的有效边界。在两种情形下，投资人全会选择具有较高值的μ或Eh（W）以及具有较低值的δ或Pr{ W≤A }。所以，均值方差有效边界通过固定δ下的最大值μ而得到，而单一账户举动组合理论有效边界则通过固定Pr{ W≤A }下的最大值Eh（W）而得到。所以，单一账户资产组合理论中的有效组合不完全等同于均值方差模型中的有效组合。

单一账户资产组合理论的内容

如果投资人期间0的财富为W0，他的目的在于使期间1的预期财富Eh（W）高达最大化 。

定理1，令单一账户证券组合选择模型为：

目标：max：Eh（W）=Σri Wi

条件：Pr{ W≤A }≤α

Σvi Wi ≤W0

其中，Σvi Wi ≤W0 是预算制约条件。模型假定状态按顺序排列，以使vi/pi 相应以i递减。在此假定下可得其最优解为：

Wi =0，当i不属于T时

Wi = A，当i属于T时\{sn}

Wn = （ W0 －Σvi Wi ）/vn ，当W0 > vn A时，胜过A，式中的加和从1到n－1。T是一个状态子集，包含第n种状态sn ，且Pr{ T }≥α，但是T中不存在真子集T’使Pr{ T’}≥α。

定理1给出了一种有效的BPT-SA的处理方案，A或者α要高达一个充足高的值，就不或许受几率的制约，所以，最佳的处理方案并没有存在。

定理2、在离散状态的例子中，均值方差有效组合具有下方的形式：

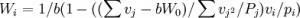均值方差有效组合

其中b是一个正的常数。

定理3、假使在BPT-SA有效组合中，起码有三种状态都具有正的消费特质，vi/pi 清晰的价值，那么，这个组合就不是均值方差有效组合。

自此可以确定单一账户举动组合理论有效边界。它就是在Pr{ W≤A }≤α的约束条件下由很多Pr{ W≤A }值和对应的最大值Eh（W）所组成的有序数对在（Eh（W），Pr{ W≤A }）平面上绘出的曲线。投资人将通过有效边界最大化函数U（Eh（W），D（A））来选择最优证券组合。

从模型解的形式可以看出单一账户举动组合理论有效证券组合收益的分布形式。其收益有三种或许的结果：0，A，好于A的值Wn。该种收益分布相似于由收益为A或0的无风险债券和收益为Wn 的彩票所组成的组合的收益分布。这与弗里德曼和萨维奇所观察到的民众同期买入保险和彩票的现象是统一的。该种同期性正是单一账户举动组合理论有效证券组合的表征。

在均值方差模型中，投资人的偏好可以用函数μ－δ2/d来表明，d表明风险容忍度。在这里，对待风险的立场由单一的变数d来衡量。而在SP/A理论中，风险是多维的，其有效边界承受五个风险度量参数的影响。它们是：

qs ，用来测量害怕的程度（对安全的需要）；

qp ，用来测量期望的程度（对潜力的需要）；

A，期望水平；

δ，用来决定害怕与期望的相对强弱；

γ，用来决定获取与害怕和期望有关的期望水平的欲望程度。

这五个参数值的改变全会会更改投资人对证券组合的选择。