多重账户资产组合理论(BPT-MA)
多重账户资产组合理论简述
多重账户资产组合选择模型是建立在期望理论之上的。Shefrin和Statman(2000)提出投资人具有两个心理账户,分别对应高、低两个期望值,代表投资人既想避免贫困,又期望变得富裕的愿望。高、低期望值兼而有之的资产组合常常被描述为分层的金字塔,投资人在底层和顶层之间分配财富,底层的财富是为了避免贫困,顶层的财富是为了变得富裕。投资人的目标就是将现有财富W0在两个账户间分配以使整体效用高达最大。
多重账户资产组合理论的内容
如果低期望帐户的效用函数为Cobb-Douglas函数:
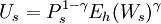 公式1
公式1
Eh(Ws)γ ,其中Ps代表达不足低期望水平As的几率,Ws代表财富,而γ是一个非负权重参数。相似的,高期望账户的效用函数为:
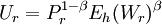 公式
公式
其中各参数含义与前式对应。则可假定投资人的效用函数是低期望账户的效用函数与高期望账户的效用函数的联合体为:
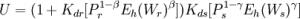 公式2
公式2
从投资人效用函数的形式可以看出,当低期望账户的效用为0时,投资人的效用也为0;而当高期望账户的效用为0时,投资人的效用却不必为0。这代表着财富中的一部分将首先分配给低期望账户。假使卖空被允许,投资人在他的高期望账户里或许会持有某些证券的空头,而在低期望账户里相应持有其多头。原因在于两种心理账户之间缺乏统一性,协方差被忽视了。
总之,投资人将心理账户与目标相匹配。两个心理账户不统一,最大化投资人整体效用的做法将令使低期望账户中的组合比高期望账户中的组合看上去更像无风险债券,而与之相反,高期望账户里的组合更像彩票。
BPT与MPT的分析框架是类似的,均为在一定风险下谋求最大收益,在风险与收益平面内构造有效边界,并依据效用函数分析最优组合。但二者也存在较大差异,这体当下风险度量与将来收益的确定方面,该种差异首要因为对投资人心理与举动理解的不同。
MPT中的投资人对将来各种不同前景显现的几率以及相应的期望值能够执行客观公正的估价,而且由于投资人均是理性人,他们的估值也无差异。其直接结果便是造成一条供所有投资人选择的有效边界,这条有效边界不会因人而异。但BPT中的投资人是正常人,他对将来的预期会承受害怕、期望、期望等感情原因的影响,而且不同的投资人其影响程度有所不同。该种差异体当下对将来收益的期望均值估值上的不同,悲观者会让之偏低而乐观者会让之偏高,与此对应的是每位投资人都有属于自己的有效边界。
MPT 以预期效用理论为基础,投资人均是风险厌恶者,对待风险的立场始终不变,其差别导致厌恶程度不同,以效用函数u-δ2 /d 中的d表达风险容忍程度。而BPT以期望理论为基础,投资人是损失厌恶者,他们一面谋求安全保证,另一面又追求高风险以期望获取高收益。其投资人对风险的立场是多重度量的,用qs 、qp 、A、δ、γ五个参数来描述。受于假定投资人对待风险立场的不同,因此两个理论对风险的度量也有所不同。MPT以δ或δ2 度量风险,而BPT以几率Pr{ W≤A }度量风险。
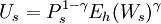 公式1
公式1
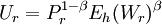 公式
公式
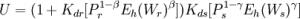 公式2
公式2
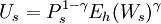 公式1
公式1
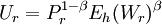 公式
公式
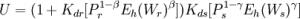 公式2
公式2