菲波纳契数列又称“菲波纳契神奇数列”，是由13世纪的意大利数学家菲波纳契提出的，当时是和兔子的繁殖困难相关的，它是一个很重要的数学模型。这个困难是：有小兔一对，若第二个月它们成年，第三个月生下小兔一对，以后每月生产一对小兔，而所生小兔亦在第二个月成年，第三个月生产另一对小兔，以后亦每月生产小兔一对，假定每产一对小兔必为一雌一雄，且均无死亡，试问一年后共有小兔几对？
对于n=1，2，……，令Fn表明第n个月开始时兔子的总对数，Bn、An分别是未成年和成年的兔子（简称小兔和大兔）的对数,则Fn = An + Bn。
依据题设，有：
显然，F1 = 1，F2 = 1，而且从第三个月开始，每月的兔子总数正好等于它前面两个月的兔子总数之和，于是按此规律我们得到一个带有初值的递推关系式：
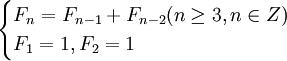
若我们规定F0 = 1，则上式可变为：
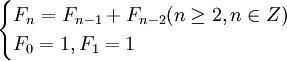
这就是Fibonacci数列的一般定义，也就是数列1、1、2、 3、5、8、13、 21、34、55、89、144、233、377、610、987、1597……，直至无限。这串数列的特点是：其中任一个数均为前两数之和。从上述数字看，系列由1、2、3开始，继而造成无限数字系列；这与《道德经》第四十二章：“道生一，一生二，二生三，三生万物”所包含的道理不谋而合。由神奇数字演变出来的比率（即黄金比率，golden ratio），是 0.236、0.382、0.5、0.618、0.764、1.618、2.618 等，上述比率有助推断将来高位或低位。
这个兔子困难是意大利数学家莱昂纳多·菲波纳契（Leonardo Fibonacci）在他所著的《算盘全集》中提出的，所以这个数列称作菲波纳契数列，其中每一项称作Fibonacci数。
它的通项是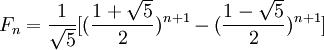
，由法国数学家比内（Binet）求出的。
菲波纳契数列的特点
菲波纳契数列既谓神奇数字，上述数字自有神奇之处，其特点包含：
1、从第三项起，任何一个数字均是其前两个数字的和数，比如1+1=2；1+2=3；2+3=5；3+5=8；5+8=13；8+13=21；13+21=34等。
2、任何两个相隔的数字彼此顺序相除或倒转相除，所得数字分别靠近0.382及2.618。
靠近0.382比率，比如：8÷21=0.381；13÷34=0.382；21÷55=0.382等。
靠近2.618比率，比如：21÷8=2.625；34÷13=2.615；55÷21=2.619等。
3、除首四个数字（1、1、2、3）外，两个相邻数字彼此相除，所得数字分别靠近0.618及1.618比率。
靠近0.618比率，比如：5÷8=0.625；8÷13=0.615；13÷21=0.619等。
靠近1.618比率，比如：8÷5=1.6；13÷8=1.625；21÷13=1.615等。
在股市中，菲波纳契数列的作用在于预期将来行情的升降幅。若配合波浪理论，可以神奇数字计算出预期的升降幅度；藉此，投资人可推测短线、中线或长线行情的支持位或压力位，及早趁低吸纳或趁早沽出。