复合套期保值

什么是复合套期保值

采取多种套期保值(如采取多种期货合约或期权)的套期保值为复合套期保值。

复合套期保值原理

民众一般把价格风险划分为系统风险和非系统风险两类。系统风险是指对市场上所有资产价格都有影响的风险，包含政策影响、宏观经济原因等各种风险。非系统风险是指只对单个资产造成影响的风险。同样，投资人所构筑的投资管理也面对着系统风险和非系统风险。现假定投资管理中包含n项资产，每项资产在投资管理中所占权重为 $ω i$ , $ω j$ ,第i,j种期货合约的方差分别为 $δ i$ , $δ j$ ,价格为 $ρ i, j$ ,依照Markowitz投资管理理论，该组合的收益方差即价格风险

$\delta^2=\sum_{i=1}^n\sum_{j=1}^n\omega_i\omega_j\delta_i\delta_j\rho_i,j=\sum_{i=1}^n\omega_i^2\delta_i^2+2\sum_{i />j}^n\sum_{j=1}^n\omega_i\omega_j\delta_i\delta_j\rho_{i,j}$

由上式可目睹，伴随组合中包含的资产数n渐渐扩大，非系统风险渐渐减小，并最终趋近于零.所以，非系统风险可通过组合的充分分散化而清除掉.但是系统风险却不能分散，伴随n渐渐变大，系统风险将趋于投资管理所包含的任意两项资产协方差的平均值.

对于侧重投资证券市场的投资人，其利用股指期货执行套期保值的目的首要是规避系统风险，其原理可简单表述为：假定某投资人持有一单位证券组合A，其价格为S，Beta系数为 $β$ ， $r s$ 是该组合的收益率；一单位股票指数组合为M， $r M$ 是股票指数组合的收益率.则该投资人持有的证券组合收益就分别包含系统风险 $β r m$ 和非系统风险导致的收益 $r u$ ，即

$r s = β r M + r u$

$(r_s=\frac{\triangle S}{S},r_M=\frac{\triangle M}{M})$ (1)

式(1)两边同乘以S,可以推出

$\triangle S=S\beta(\frac{\triangle M}{M})+Sr_u$

假定投资人买入 $n f$ 单位股指期货合约对该组合执行套期保值，则新的组合价值

$V=\triangle S+n_f\triangle f$ （２）

(2)式中，V为新的组合价值，f为股指期货合约价值， $n f$ 就是套期保值率。

为使证明简单化，如果期货合约价格改变与股票指数改变统一，则 $n f$ 可直接用回归方法求得，即

$\begin{cases}\frac{\triangle M}{M}=\frac{\triangle f}{f}\\n_f=-\beta(\frac{S}{f})\end{cases}$ （３）

把式（3）代入式（2）中，可得

$V = Sr u$ （４）

式（４）显示，在运用股指期货合约执行套期保值后，新的组合已完全刨去了系统风险对价格的影响，组合价值还剩下非系统风险的影响$而非系统风险可通过组合分散化清除，进而锁定整个组合的风险水平.诚然，这导致最基本的一种套期保值方法，即完全套期保值方法.在实践中，投资人一般只对证券组合执行部分套期保值，如投资人一般期望能保留系统风险对价格的有利影响，而清除其不利的影响，进而可构筑出各种更为高级和复杂的套期保值方法.

复合套期保值是一种采取多种期货合约执行套期保值的方法，而简单套期保值只采取单种指数期货合约执行套期保值，简单套期保值可以看作是复合套期保值的特殊情况.

与证券市场一样，股指期货市场风险也包含系统风险和非系统风险两种$当采取简单套期保值方法时，非系统风险会影响股指期货合约价格波动，进而减弱期货合约价格与股票指数的有关程度，并最终影响套期保值效果.非系统风险可通过组合分散化清除，而复合套期保值基本原理正是利用了分散化相伴而来的非系统风险降低，进而比简单套期保值高达许多地降低非系统风险的目的，保证了复合后的套期保值工具与股票指数的有关程度，使复核后的套期保值更具效率。

与有价证券组合不同，复合套期保值并没有能完全清除非系统风险，这首要是由于现实的股指期货市场能够上市而且同期执行交易的合约品种一般只有几种，能够运用的交叉套期保值工具相对不足$但是，这并没有影响复合套期保值方法运用上的优越性，由于非系统风险在分散化的初始阶段会有明显下滑，进而一个仅包含两三种不同期货合约的复合套期保值也能供应明显的好处。

复合套期保值的优越性

复合套期保值能更大限度地减弱非系统风险，具有比简单套期保值更好的套期保值效果。对此，可用套期保值绩效评价办法来做简单对比如下：首先可以计算出每一种股指期货合约的套期保值率 $n i$ ，并定义每一单位“调整后的期货合约”等于n_i份原有的股指期货合约。比如第i种期货合约的最优套期保值率为2，则一单位调整后的套期保值工具就由两单位的第"种期货组成。如此，所有经历调整后的股指期货合约的最优套期保值率就均是1，进而整个复合套期保值的基差方差:

$\delta_c^2=\sum_{i=1}^n\sum_{j=1}^n\omega_i\omega_j\rho_{i,j}$

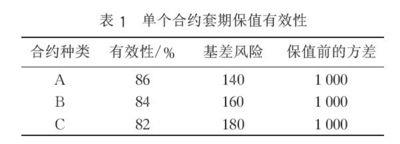
假定股指期货市场有不同到期月份的)A,B和C三种期货合约，每种合约的套期保值成本相同,另外，如果每一个指数期货合约套期保值的有效性和基差方差如1表所示。

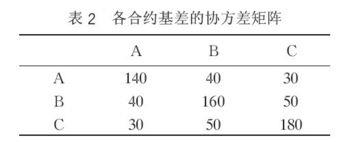
假使投资人采取简单套期保值方法，就会选用合约A作为套期保值工具,假定合约A,B和C基差的协方差矩阵已知，见表2.

汇外网 - 全球专业的黄金外汇门户导航行情资讯网站

当下假定投资人在获知各合约基差的协方差矩阵后，决定采取复合套期保值方法，而且每个合约的权重相同（均是1/3），于是值得计算出复合套期保值后的基差方差

$\delta_c^2=\sum_{i=1}^3\sum_{j=1}^3\omega_i\omega_j\rho_{i,j}=(\frac{1}{3})^2*140+(\frac{1}{3})^2*160+(\frac{1}{3})^2*180+2*(\frac{1}{3})^2*(30+40+50)=80$

则复合套期保值的有效性为

$\rho^2=1-\frac{\delta_c^2}{\delta_p^2}=1-\frac{80}{1000}=92%$

所以，在假定各合约的套期保值成本相同的情形下，采取复合套期保值的有效性92%大大好于采取简单套期保值中有效性最高的83%,诚然上述方案导致做了简化处理后的情形，对于其余情形，依然可以得出相同的结果，即复合套期保值要比简单套期保值优越,

复合套期保值的的优点

从本质上表达，复合套期保值的风险减弱来因为两个方面：

(1)套期保值所固有的风险减弱；

(2)通过证券组合多样化将风险减弱。

所以可以说，复合套期保值是马柯维茨的证券组合理论在套期保值上的应用。