核心存款

什么是核心存款

核心存款又被称为无到期日存款(non-maturity deposit)或流动性存款(liquidity deposit)。对于核心存款的定义，当前仍未形成统一的标准。

美国通货监理局(Office of Comptroller of the Currency，简称OCC)觉得，所谓核心存款就是指那些能够平稳客户关系的活期和定期存款，银行可以在一定期间，一般是数年内运用这些资金。

Becher(1962)，Parson(1972)以及Flannery(1982)觉得，核心存款是指受于存在整置成本(setup cost，又译为起动成本、整备成本等)和交易投资成本而使银行和储户都愿意继续持有的那部分存款。

McGuire(1995)从储户的角度给出了如下的定义：核心存款是指那些首要用于满足交易支付需求且可以随时提取的存款。

纵观上述定义，笔者觉得，核心存款就是储户在银行持有的对市场利率变动不敏感且可以随时支取的那部分资金头寸。

核心存款比率

核心存款比率显现为核心存款和总资产比率以及核心存款和贷款总额的比率。

核心存款比例=核心存款/总资产

核心存款指那些相对来看比较平稳的，对利率改变不太敏感的存款，季节和经济环境对其影响也较小，所以核心存款是银行资金的平稳来源，这一比率反应了银行流动性大小；

国外对核心存款的研究

1.核心存款余额的平稳性和长期性

一般觉得，核心存款余额对利率不敏感，因此比较平稳。Becher(1962)，Oi(1962) 以及Parson(1972)发现，储户设立新帐户(在银行开设新帐户)会造成整置成本，该成本会促使银行和储户保持现有的关系。尽管从短时间来说保持该种关系对双方或许都不是最优的，但长期来说是最优选择。Flannery(1982)的结论同上述看法类似。他觉得，签署新的存款合同会同期给银行和储户都导致整置成本和学习成本。银行在资金充足时为了节约资金成本，就可降低核心存款余额。但受于存在上述成本，再加之将来的资金需求量或许较大，所以银行一般并没有愿意降低核心存款余额。对于储户来说其原理也是相同的。笔者觉得，核心存款体现了银行和储户的互利关系：银行乐意长期为储尸供应各种优质服务，而储户也愿意长期接受差于市场利率的存款收益。该种互利关系致使核心存款余额的变动不会受于外界环境的改变丽发生很大的改变，因此核心存款的余额比较平稳。

尽管核心存款余额比较平稳，但受于核心存款可以随时提取，所以它不像定期存款那样有确切的到期日，如3年。Flannery和James(1984)表示，受于储户愿意持有一定数量的核心存款来满足日常交易以及应付突发事件造成的支付需求，因此核心存款具有较长的事实到期日。但是他们仍未表示核心存款的具体到期日。对于商业银行来说，只有精准地了解每一笔资金来源的期限才可合理地安排资金贷放，才可避免显现资金闲置或不足的困难。因此仅研究核心存款余额具有较长的事实到期日是不够的，商业银行关注的是，“较长”见底有“多长”，3年依旧5年，抑或10年。所以，测度核心存款余额的事实到期日已形成学者们更深一步研究的课题。

1993年，美国学者Chambers最先给出核心存款余额的事实到期日。他的研究显示，核心存款的平均持有期是5年。在他之后仍有不少学者对这一困难也执行了研究。Morgan和Cates(1994)的实证分析显示，一般银行在8年后失去50%的核心存款储户，而在20年后则将失去所有的核心存款储户(不考虑新储户的加入)。就平均来说，核心存款的持有期为6—8年。他们的研究不仅给出了核心存款余额的事实到期日，而且还得出“核心存款消亡的进展随时间的推动而持续减弱”的重要结论。Berger和Udell(1995)的研究表明，核心存款的事实到期日约为12年，而Pennacchi(1996)的实证结果是6年。从总的看，核心存款的事实到期日约为6年。产生Berger、Udell(1995)与其余学者结论不同的首要原因在于他们选取不同性质的样本。在分析了他们所研究的银行核心存款组成比例后，笔者发现，前者的研究对象，即所选取银行的核心存款首要以个人活期存款帐户为主，而后者所研究的对象则以企业活期存款帐户为主。受于企业存款的金额较大，因此对利率的敏感性相对较高，其期限比个人活期存款短也属正常。这样看来，即使核心存款没有确切的到期日，但其事实到期日却非常长。所以，对于银行来说，核心存款余额具有平稳和长期的特性。同期，上述学者研究结论的冲突也告诉我们：在研究核心存款事实到期日的时机，应当将不同种类的核心存款，分别计算其事实到期日，如此才可得到比较精准的报告。

从表面看，核心存款利率是由商业银行直接策划的。事实上，银行在策划这一利率时仍需要考虑储户的反映和市场的情况。Whitesell(1992)和Hutehison(1995)强调了积蓄和交易功能在核心存款定价方面的重要性。他们觉得，储户的积蓄意向(与投资意向相对应)越强，核心存款的交易功能越多，则利率越低。 McGuire(1995)觉得，商业银行和储户的博弈决定核心存款的利率环境。商业银行对核心存款附加服务的质量和便利程度是储户考虑的首要原因，而储户的偏好又决定了商业银行在现行市场利率条件下策划一个最优利率。在一部分经济原因发生改变以后，以前的均衡就会被打破，于是造成新一次的博弈，最终高达一个银行和储户都不愿更改的现有策略的纳什均衡点。

当前，许多的研究汇聚在核心存款利率的特性上。Small(1990)，Harman和Berger(1991)，Neumark和 Sharp(1992)以及Ausubel(1992)，在分析了美国银行的数据统计后表示，核心存款利率具有三个基本特质：一是核心存款利率差于市场利率(一般指一年期存款或国债利率)；二是短时间内核心存款利率呈现粘性(核心存款并没有立刻对市场利率的调整做出反映，其调整存在适当的时滞)；三是从长期看核心存款利率调整趋势不对称(当市场利率上升时，核心存款利率并没有跟随上升，呈现刚性特质；当市场利率下滑时，核心存款利率跟随下滑，呈现非刚性特质)。核心存款利率差于市场利率这比较容易理解，由于核心存款的流动性要好于一年期存款和国债，因此其收益率就相对较低。而短时间内核心存款利率呈现粘性的看法是由O’Brien (2000)提出的。他觉得，从理论上讲，在外部原因影响市场利率以后，核心存款利率应该跟随发生变动。但事实上，假使市场利率上升，银行就提升核心存款利率，则会增长利息开支。为了控制成本，银行就会减弱对核心存款储户服务的质量，并降低服务种类。储户也意识到，假使存款的利息收益增长，那就不或许享受原本的优质服务，得到的便利也会降低，因此储户乐意接受原本的利率。受于银行和储户都不愿更改原本的策略，核心存款利率在短时间内就不会上升。同理，假使市场利率下滑，银行和储户也依然会采取以前的策略，核心存款利率也不会跟随下滑。所以，从事实情形来说，银行不会由于市场利率的变动而频繁调整核心存款利率，核心存款利率在短时间内具有粘性。但从长期来说，核心存款利率具有不对称调整的特性。Ausubel (1992)觉得，信息有限以及搜寻成本的存在是核心存款利率不对称调整的首要原因。其模型结论为当市场利率持续下滑时，商业银行核心存款流失的几率也非常大。而事实情形是从长期看，当市场利率持续上升时，储户受于受高利率的诱惑而持续将核心存款转向其余投资工具。Sharpe(1997)根据消费者搜寻成本的建模，解释了核心存款利率调整不对称的.原因，但他没有提出清晰的处理方案。Kahn等(1999)利用消费者的有限记忆尝试对存款利率调整执行解释，但他们依旧未能清晰解释核心存款利率为何在市场利率上升和下滑时会显现不对称调整的现象。时迄今日，还没有一名学者能够合理地解释这个困难。

国外金融机构在金融产品的定价及风险预期和防范管理方面，一般都看好于运用定量模型。但核心存款的定量分析却没有一个相似于资本资产定价模型(CAPM)的标准模型，首要原因在于核心存款缺少一个具有高度流动性的二级市场。Ausubel(1991)，Calera和Mester(1995)以及Hutchison和Pennaechi(1996)通过研究发现，核心存款之所以很难估价，是由于市场竞争不完全，商业银行一般不会将其核心存款卖出给其余银行。同期，搜寻和转换成本、监管壁垒以及逆向选择困难等也致使核心存款的估价变得愈加问题。

核心存款的估算

1.HP滤波法原理

HP滤波法是由Hodrick和Prescott于1980年在分析美国战后的经济景气时首先提出的。该种方法被普遍地应用于对宏观经济趋势的分析研究中。HP滤波法是一种时间序列在状态空间中的分析方法，相当于对波动方差的极小化。HP滤波可以看作是一个近似的高通滤波器(High-Pass Filter)，其理论基础是时间序列的谱分析方法。谱分析方法把时间序列看作是不同频率的成分的再加上，时间序列的High-Pass滤波就是要在这些所有的不同频率的成分中，分离出频率较高的成分，去掉频率较低的成分，也即去掉长期的趋势项，而对短时间的随机波动项执行度量。

HP滤波的原理，可以表述为：

如果经济时间序列为Y={y₁,y₂,…,y_n}，趋势要素为G={g₁,g₂,…,g_n}。其中，n为样本的容量。所以，HP滤波可以将y_t(t=1,2,…n)分解为：

y_t = g_t + c_t

其中，g_t和c_t都是不可观测值。

一般的，时间序列Y中不可观测部分趋势G常被定义为下面(1)最小化困难的解：

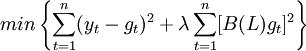
其中，B(L)是推迟算子多项式

B(L) = (L ^{− 1} − 1) − (1 − L)

将(2)代人(1)式，则HP滤波的困难就是使下面损失函数最小，即

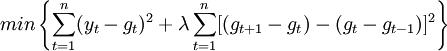
对(3)式y₁,y₂,...,y_n执行一阶求导，并令导数为0，得：

g₁:c₁ = λ(g₁ − 2g₂ + g₃)

g₂:c₂ = λ( − 2g₁ + 5g₂ − 4g₃ + g₄)

g_t:c_t = λ(g_{t − 2} − 4gt − 1 + 6g_t − 4gt + 1 + g₄)

g_{n − 1}:c_{n − 1} = λ(g_{n − 3} − 4gn − 2 + 5gn₁ − 2g_n)

g_n:c_n = λ(g_{n − 2} − 2gn₁ + g_n)

用矩阵形式表明，为：

c = λFg

F为如下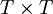系数矩阵：

通过上述公式，可以得到：

y − g = λFg

整理后，可得：

g = (λF + I) ^{− 1}y

而且，在上述F矩阵中，每一列元素之和都是零。所以，依据C=\lambda Fg可知，短时间波动之和为0。即：

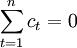
最小化困难用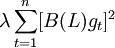来调整趋势的改变。而且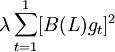，的取值伴随λ的放大而放大。不同的λ值决定了不同的随机波动方式和不同的平滑程度。当λ = 0时，有g_t = y_t，满足最小化困难的趋势等于序列Y；伴随λ的增长，预期的趋势越光滑；当λ→∞时，预期的趋势也就靠近于线性函数，这时，HP滤波就退化为用最小二乘法预期趋势。从统计意义上讲，λ的值的选取是任意的，由于任何一个非稳定时间序列都可以分解形成无多个非稳定趋势成分与稳定周期成分的组合。但λ的取值决定着趋势要素对事实序列的追踪程度和趋势光滑度之间的权衡选择。分别用 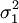和 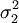表明时间序列中趋势成分和周期成分的标准差，那么，λ的最优取值即为 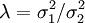。依据一般经验，\lambda的取值如下：

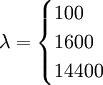
100，年度报告；1600，季度报告；14400，度报告

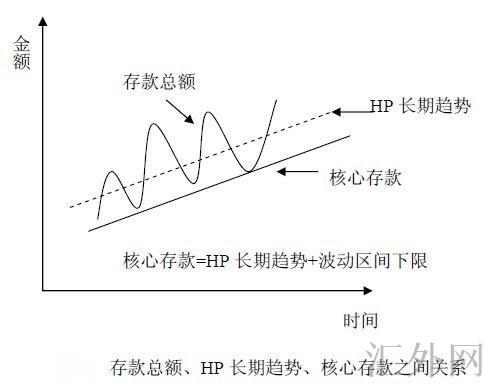
采取HP滤波方法计算出来的长期趋势反应了商业银行存款总额变动的平均状态。事实存款总额总是环绕长期趋势而上下波动, 且由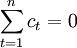可以得知，各期波动存款之和为零。而我们所要求的核心存款是指存款中长期平稳部分, 波动存款在核心存款之上浮动。核心存款与波动存款之间具相关系：

波动存款=存款总额-核心存款

所以, 用HP滤波求出的长期趋势成分和短时间波动成分并没有是我们所需要的核心存款和波动存款，我们仍需要在此基础上做更深一步计算,以得出平稳的核心存款金额。

为此，本文把用HP滤波法计算出来的长期趋势做下探，进而以适当的几率保确认际存款总额总是在核心存款之上波动。

如果由HP滤波求得的波动部分c_t满足正态分布N(μ , σ²)，其中μ为c_t的期望，σ²为方差。则由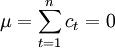 和 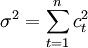即可求得N(μ，σ²)。取存款总额在核心存款之上的几率为置信水平(1- α)，满足置信水平(1- α)的区域为(-C,C)，则有：

26344.png">

受于α、σ都是已知量，所以，可以反求出C。将HP滤波法求得的平稳部分g_t朝下平移C即得到核心存款：

核心存款= g_t − C

如图所示，存款总额、核心存款与通过HP滤波方法得到的长期趋势之间具有如下关系：

参考文献

↑ ^1.01.1 吴许均.国外核心存款研究总括