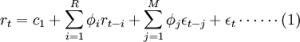 GARCH
GARCH
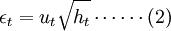 GARCH
GARCH
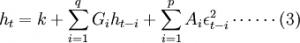 GARCH
GARCH
其中ht为条件方差,ut为独立同分布的随机变量,ht与ut互相独立,ut为标准正态分布。(1)式称为条件均值方程;(3)式称为条件方差方程,表明时间序列条件方差的改变特质。为了适应收益率序列经验分布的尖峰厚尾特质,也可如果 服从其余分布,如Bollerslev (1987)如果收益率服从广义t-分布,Nelson(1991)提出的EGARCH模型采取了GED分布等。此外,很多实证研究显示收益率分布不但存在尖峰厚尾特性,而且收益率残差对收益率的影响还存在非对称性。当市场承受负打击时,股价下挫,收益率的条件方差扩大,致使股价和收益率的波动性更大;反之,股价上升时,波动性减小。股价下挫致使公司的股票价值下滑,假使如果公司债务不变,则公司的财务杠杆上升,持有股票的风险提升。所以负打击对条件方差的该种影响又被称作杠杆效应。受于GARCH模型中,正的和负的打击对条件方差的影响是对称的,所以GARCH模型不能刻画收益率条件方差波动的非对称性。
GARCH模型的成长 为了衡量收益率波动的非对称性,Glosten、Jagannathan与Runkel(1989)提出了GJR模型,在条件方差方程(3)中加入负打击的杠杆效应,但仍采取正态分布如果。Nelson(1991)提出了EGARCH模型。Engle等(1993)利用信息反映曲线分析比较了各种模型的杠杆效应,觉得GJR模型最好地刻画了收益率的杠杆效应。Glosten、Jagannathan与Runkel(1993)分析比较了各种GARCH-M模型,表示不同的模型设定会致使条件方差对收益率造成正或负的不同影响, GARCH模型的缺陷 受于GARCH (p,q)模型是ARCH模型的扩展,所以GARCH(p,q)同样具有ARCH(q)模型的特点。但GARCH模型的条件方差不仅是落后残差平方的线性函数,而且是落后条件方差的线性函数。 GARCH模型适合在计算量不大时,方便地描述了高阶的ARCH过程,因此具有更大的适用性。但GARCH(p,q)模型在应用于资产定价方面存在下方的不足: ①GARCH模型不能解释股票收益和收益改变波动之间显现的负有关现象。GARCH(p,q)模型假定条件方差是落后残差平方的函数,所以,残差的符号不影响波动,即条件方差对正的单价改变和负的单价改变的反映是对称的。但是在经验研究中发现,当利空消息显现时,即预期股票收益会下滑时,波动趋向于放大;当有利于消息显现时,即预期股票收益会上升时,波动趋向于减小。GARCH(p,q)模型不能解释该种非对称现象。 ②GARCH(p,q)模型为了保证非负,假定(2)式中所有系数均大于零。这些约束隐含着的任何落后项放大全将增长因此消除了的随机波动举动,这致使在预期GARCH模型时或许显现震荡现象。