跨期资本资产定价模型(Intertemporal Capital Asset Pricing Model 或 Intertemporal CAPM,简称ICAPM),也称瞬时资本资产定价模型
什么是跨期资本资产定价模型 在资产定价理论中的其他重要如果是:证券市场总是在接连过程中,在这一如果前提下,Merton(1969,1971)将CAPM发展为跨期资本资产定价模型(ICAPM),同样在信息对称、无摩擦的市场中,资产价格的改变符合Ito过程,在该种条件下,资产的单价与投资人的效用偏好无关。在随后的研究中Merton(1973)和Black(1973)应用以上接连时间模型成功地得到了期权定价公式,这一公式后来被大批的实证研究所确认,而且被普遍在实践中应用。 传统CAPM中的一个核心如果是投资人只考虑单一投资期,很显然这是一个不现实的如果。为了放松这一如果,把CAPM模型扩展到动态环境中,默顿(1969,1972,1973)构建了一个接连时间的投资管理与资产定价的理论框架,提出了一个跨期CAPM (ICAPM)。 默顿觉得,投资人对风险证券的需求包含两部分:马科维茨的静态资产组合最优化困难中的均值一方差成分和规避对投资机会集的不利打击的需求。当投资机会集发生不利变动,而同期又存在一种收益率很高的证券时,每一个理性的投资人全将期望购入该种证券作为一种套期保值措施。该种套期保值需求的增长同期也致使了该证券均衡价格的上升,推导ICAPM的核心就是在资产定价方程中反应该种套期保值需求。 在ICAPM中,投资人的决策将最大化整个投资期的效用,即:
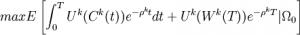 ICAPM
ICAPM
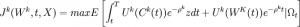 ICAPM
ICAPM
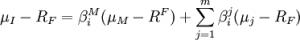 ICAPM
ICAPM
